Proposition Logic - Winerva Blog

PS. Writing AI that’s actually able to understand this sort of logic.

Propositional logic (also called proposition logic, sentential logic, or Boolean logic) is a branch of logic that deals with propositions and their truth values—true or false.

🔹 Proposition Symbols P, Q, R

Symbol	Meaning
P	A proposition (a basic statement)
Q	Another proposition
R	Yet another proposition

These are just placeholders for any statements we want to reason about logically.

🔹 Key Concepts

Proposition: A statement that is either true (T) or false (F), but not both.
- Example:
  - “It is raining.” → a proposition
  - “Close the door.” → not a proposition (it’s a command)
Logical Connectives (used to build compound propositions):
- ¬ (NOT): Negation
  - ¬P is true if P is false.
- ∧ (AND): Conjunction
  - P ∧ Q is true if both P and Q are true.
- ∨ (OR): Disjunction
  - P ∨ Q is true if at least one of P or Q is true.
- → (IMPLIES): Conditional
  - P → Q is false only if P is true and Q is false.
- ↔ (IFF): Biconditional
  - P ↔ Q is true if P and Q have the same truth value.

🔹 Propositional Logic Symbols Table

Symbol	Name	Meaning in English	Example	Example Meaning
¬P	Negation	“Not P”	¬P	“It is not raining.”
P ∧ Q	Conjunction	“P and Q”	P ∧ Q	“It is raining and the ground is wet.”
P ∨ Q	Disjunction	“P or Q” (inclusive or)	P ∨ Q	“It is raining or the ground is wet.”
P → Q	Implication	“If P, then Q”	P → Q	“If it rains, then the ground is wet.”
P ↔ Q	Biconditional	“P if and only if Q”	P ↔ Q	“It rains if and only if it’s cloudy.”

🔹model

assignment of a truth value to every propositional symbol (a “possible world”)

P: It is raining
Q: It is a Tuesday
{P = true, Q = false}

🔹 Knowledge base

a set of sentences known by a knowledge-based agent, allowing the AI to access the knowledge base. AI would like to use that information in the knowledge base to be able to draw conclusions about the rest of the world.

🔹 Entaliment

P ⊨ Q

It means: “Q is logically entailed by P“
Or: “If P is true, then Q must also be true.”

🔹 inference

the process of deriving new sentences from old ones.

P: It is a Tuesday.

Q: It is raining.

R: Harry will go for a run.

KB: (P ^ ¬Q) → R

So. P ¬Q Inference: R

Knowledge Base Flow Chart,propositional logic — Knowledge Base

🔹 Knowledge Base Example: Clue Game

Proposition Symbols

People	Rooms	Weapons
Colonel Mustard	ballroom	knife
Professor Plum	kitchen	revolver
Miss Scarlet	library	wrench

A propositional logic representation of this game of Clue

(Colonel Mustard v Professor Plum v Miss Scarlet)
(ballroom v kitchen v library)
(knife v revolver v wrench)
¬ Professor Plum
¬Colonel Mustard v ¬library v ¬revolver

import termcolor

from logic import *

mustard = Symbol("ColMustard")
plum = Symbol("ProfPlum")
scarlet = Symbol("MsScarlet")
characters = [mustard, plum, scarlet]

ballroom = Symbol("ballroom")
kitchen = Symbol("kitchen")
library = Symbol("library")
rooms = [ballroom, kitchen, library]

knife = Symbol("knife")
revolver = Symbol("revolver")
wrench = Symbol("wrench")
weapons = [knife, revolver, wrench]

symbols = characters + rooms + weapons


def check_knowledge(knowledge):
    for symbol in symbols:
        if model_check(knowledge, symbol):
            termcolor.cprint(f"{symbol}: YES", "green")
        elif not model_check(knowledge, Not(symbol)):
            print(f"{symbol}: MAYBE")

# There must be a person, room, and weapon.
knowledge = And(
    Or(mustard, plum, scarlet),
    Or(ballroom, kitchen, library),
    Or(knife, revolver, wrench)
)
print(knowledge.formula())

# There must be a person, room, and weapon.
knowledge = And(
    Or(mustard, plum, scarlet),
    Or(ballroom, kitchen, library),
    Or(knife, revolver, wrench)
)

#print(knowledge.formula())
check_knowledge(knowledge)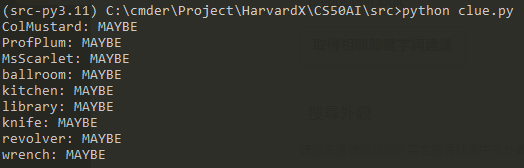

# There must be a person, room, and weapon.
knowledge = And(
    Or(mustard, plum, scarlet),
    Or(ballroom, kitchen, library),
    Or(knife, revolver, wrench)
)

# Initial cards
knowledge.add(And(
    Not(mustard), Not(kitchen), Not(revolver)
))

check_knowledge(knowledge)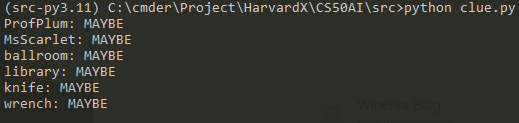

# There must be a person, room, and weapon.
knowledge = And(
    Or(mustard, plum, scarlet),
    Or(ballroom, kitchen, library),
    Or(knife, revolver, wrench)
)

# Initial cards
knowledge.add(And(
    Not(mustard), Not(kitchen), Not(revolver)
))


# Unknown card
knowledge.add(Or(
    Not(scarlet), Not(library), Not(wrench)
))

check_knowledge(knowledge)

# There must be a person, room, and weapon.
knowledge = And(
    Or(mustard, plum, scarlet),
    Or(ballroom, kitchen, library),
    Or(knife, revolver, wrench)
)

# Initial cards
knowledge.add(And(
    Not(mustard), Not(kitchen), Not(revolver)
))


# Unknown card
knowledge.add(Or(
    Not(scarlet), Not(library), Not(wrench)
))

# Known cards
knowledge.add(Not(plum))

check_knowledge(knowledge)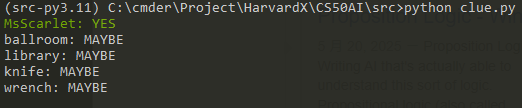

# There must be a person, room, and weapon.
knowledge = And(
    Or(mustard, plum, scarlet),
    Or(ballroom, kitchen, library),
    Or(knife, revolver, wrench)
)

# Initial cards
knowledge.add(And(
    Not(mustard), Not(kitchen), Not(revolver)
))


# Unknown card
knowledge.add(Or(
    Not(scarlet), Not(library), Not(wrench)
))

# Known cards
knowledge.add(Not(plum))
knowledge.add(Not(ballroom))
 
check_knowledge(knowledge)

AI found where the murderer committed the crime and what weapon he used.

🔹 Knowledge Base Example: Logic Puzzles

Harry Potter Sorting Test, propositional logic

proposition symbols, propositional logic

from logic import *

people = ["Gilderoy", "Pomona", "Minerva", "Horace"]
houses = ["Gryffindor", "Hufflepuff", "Ravenclaw", "Slytherin"]

symbols = []

knowledge = And()

for person in people:
    for house in houses:
        symbols.append(Symbol(f"{person}{house}"))

# Each person belongs to a house.
for person in people:
    knowledge.add(Or(
        Symbol(f"{person}Gryffindor"),
        Symbol(f"{person}Hufflepuff"),
        Symbol(f"{person}Ravenclaw"),
        Symbol(f"{person}Slytherin")
    ))

# Only one house per person.
for person in people:
    for h1 in houses:
        for h2 in houses:
            if h1 != h2:
                knowledge.add(
                    Implication(Symbol(f"{person}{h1}"), Not(Symbol(f"{person}{h2}")))
                )

# Only one person per house.
for house in houses:
    for p1 in people:
        for p2 in people:
            if p1 != p2:
                knowledge.add(
                    Implication(Symbol(f"{p1}{house}"), Not(Symbol(f"{p2}{house}")))
                )

knowledge.add(
    Or(Symbol("GilderoyGryffindor"), Symbol("GilderoyRavenclaw"))
)

knowledge.add(
    Not(Symbol("PomonaSlytherin"))
)

knowledge.add(
    Symbol("MinervaGryffindor")
)

for symbol in symbols:
    if model_check(knowledge, symbol):
        print(symbol)