The O-ring is a circular gasket used for sealing applications. It is typically made of rubber, silicone, or other elastomeric materials. O-rings are designed to sit in a groove and get compressed between two surfaces to create a tight seal, preventing leaks of fluids or gases.
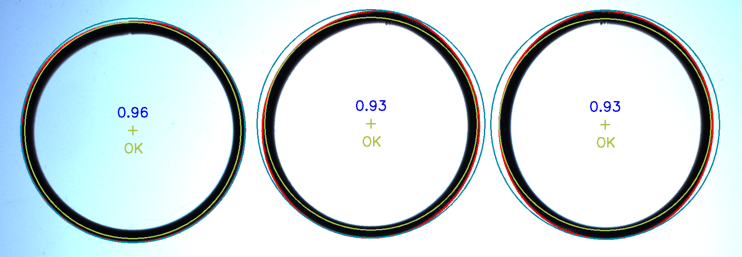
There are three O-rings in the picture. The left one is good, and the other two are defective. Intuitively, it is detected through roundness, but in practice, the basic definition of roundness of the image algorithm does not conform to the practical use.

Common Roundness Metrics:
1️⃣ Circularity (Roundness Ratio)
One of the simplest and most widely used metrics: Circularity=4π×AreaPerimeter2\text{Circularity} = \frac{4\pi \times \text{Area}}{\text{Perimeter}^2}Circularity=Perimeter24π×Area
- Perfect Circle: Circularity = 1
- More Deformed Shape: Circularity < 1
- Used in blob analysis, object recognition, and quality control.
def compute_roundness(contour):
"""
Computes the roundness (circularity) of a contour.
Circularity = 4 * pi * (Area) / (Perimeter^2)
"""
area = cv2.contourArea(contour)
perimeter = cv2.arcLength(contour, True)
if perimeter == 0:
return 0 # Avoid division by zero
circularity = (4 * np.pi * area) / (perimeter ** 2)
return circularityWe designed a sensor probe according to ISO 12181-2:2011 to contact the outer contour of the product to detect the change in the radius of the circle.
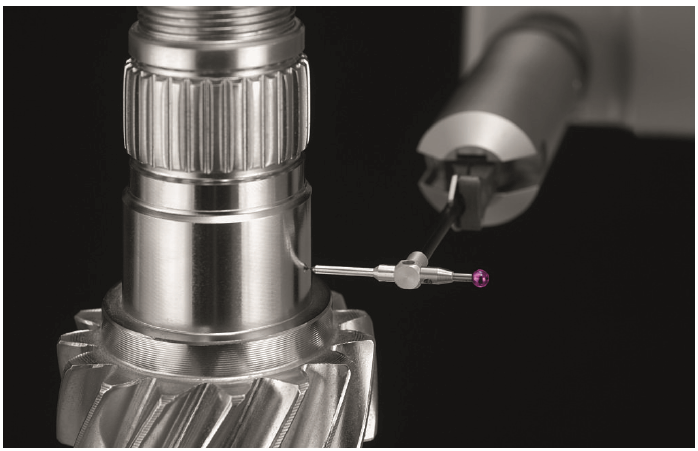
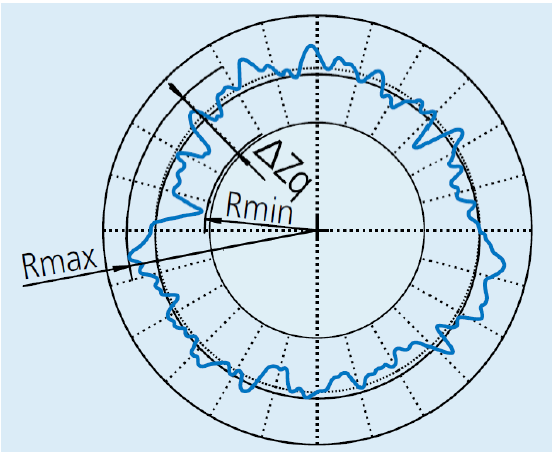
We write an imaging program to detect the outer contour of the product, see the change in radius, find the maximum and minimum radius to judge the quality of the product. ratio = min_radius / max_radius
# Find the minimum enclosing circle for the outer contour
outer_center, outer_radius = cv2.minEnclosingCircle(contour)
outer_center = (int(outer_center[0]), int(outer_center[1]))
outer_radius = int(outer_radius)
cv2.drawContours(frame, [contour], -1, (0, 0, 255), 2)
oring_image = np.zeros_like(binary_image)
cv2.drawContours(oring_image, [contour], -1, (255, 255, 255), 1)
# Start from the outer center and find the largest circle within the contour
radius = 1
while radius <= outer_radius:
circle_mask = np.zeros_like(binary_image)
cv2.circle(circle_mask, outer_center, radius, 255, thickness=1)
# Check for overlap between the generated circle and the contour
overlap = cv2.bitwise_and(circle_mask, oring_image)
if np.any(overlap > 0):
inner_radius = radius
inner_center = outer_center
break
radius += 1
ratio = round(inner_radius / outer_radius, 2)But the actual data shows that there is not much difference between good and defective products. Is there a better way?
We thought of dividing the outer contour into 10 equal parts and using the line segments of each part to fit the circle, because if the curvature of each line segment is very different, it means that there is a problem with our product. We judge good and bad products by the ratio of the maximum radius to the minimum radius of these ten fitting circles.
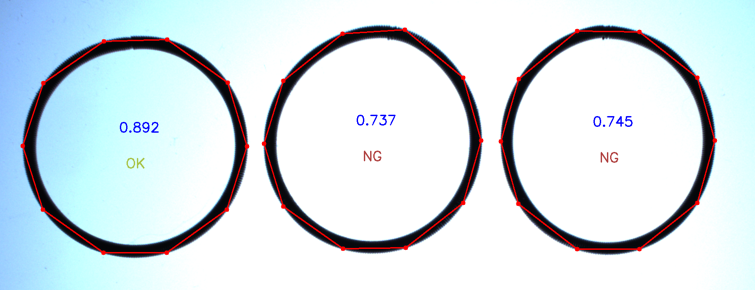
You can see that each O-ring is divided into 10 segments. In practice, 10 segments are obtained by dividing the line every 36 degrees starting from 0 degrees.
You can see from the figure that the curvature of each segment is different
📌Using the Least Squares Method to solve equations.
Using NumPy 的 np.linalg.lstsq(A, b, rcond=None) Solving the least squares problem:
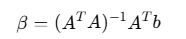
This will find the best match for your data. C,D,EC, D, EC,D,E。
📌Calculating the circle center and radius.
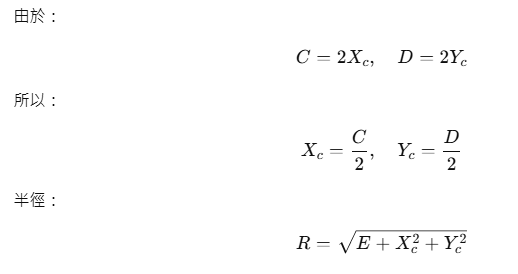
import numpy as np
def fit_circle_algebraic(points):
"""
Fitting a circle using the Algebraic Method
:param points: NumPy array of 2D points, shape (N, 2)
:return: (Xc, Yc, R) coordinates of the center and radius of the fitted circle
"""
x = points[:, 0] # Get all x coordinates
y = points[:, 1] # Get all y coordinates
# Constructing a linear system of equations Ax = b
A = np.column_stack((2 * x, 2 * y, np.ones_like(x))) # (N, 3) 矩陣
b = x**2 + y**2 # (N,) vector
# Ans: Ax = b
C, D, E = np.linalg.lstsq(A, b, rcond=None)[0] #Solving the least squares problem
# Calculate the center and radius of a circle
Xc = C / 2
Yc = D / 2
R = np.sqrt(E + Xc**2 + Yc**2)
return (Xc, Yc), R# The coordinates of each segment point
points = np.array([
[1, 7], [2, 6], [5, 8], [7, 7], [9, 5],
[7, 3], [5, 2], [2, 3], [1, 5]
])
# Calculate the fitted circle of this line segment
center, radius = fit_circle_algebraic(points)
print("圓心:", center)
print("半徑:", radius)The program logic is currently being tested and verified on the production line. This article will be updated with further results.
10 equal parts

5 equal parts
