Scipy常態分佈(normal distribution)

在SciPy的stats模塊中，norm代表正態分佈，也被稱為高斯分佈。正態分佈是一種連續概率分佈，其在平均值周圍對稱。

SciPy中的norm對象表示具有指定均值（loc）和標準差（scale）的正態分佈。它提供了各種方法來處理正態分佈，例如計算概率密度函數（PDF）、累積分佈函數（CDF）、生成隨機樣本等。

在提供的代碼中，norm用於創建一個具有均值（loc）為0和標準差（scale）為1的正態分佈對象。然後，使用這個分佈對象（dist）計算PDF、CDF，並從正態分佈生成隨機樣本。

import numpy as np
from scipy.stats import norm
x = np.linspace(-5, 5, 1000)
dist = norm(loc=0, scale=1)
pdf = dist.pdf(x)
cdf = dist.cdf(x)
sample = dist.rvs(500)
# Plot PDF
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label='PDF')

# Plot CDF
plt.plot(x, cdf, label='CDF')

# Plot histogram of samples
plt.hist(sample, bins=30, density=True, alpha=0.5, label='Sample Histogram')

# Add labels and legend
plt.xlabel('x')
plt.ylabel('Probability')
plt.title('PDF, CDF, and Sample Histogram of Normal Distribution')
plt.legend()

# Show plot
plt.grid(True)
plt.show()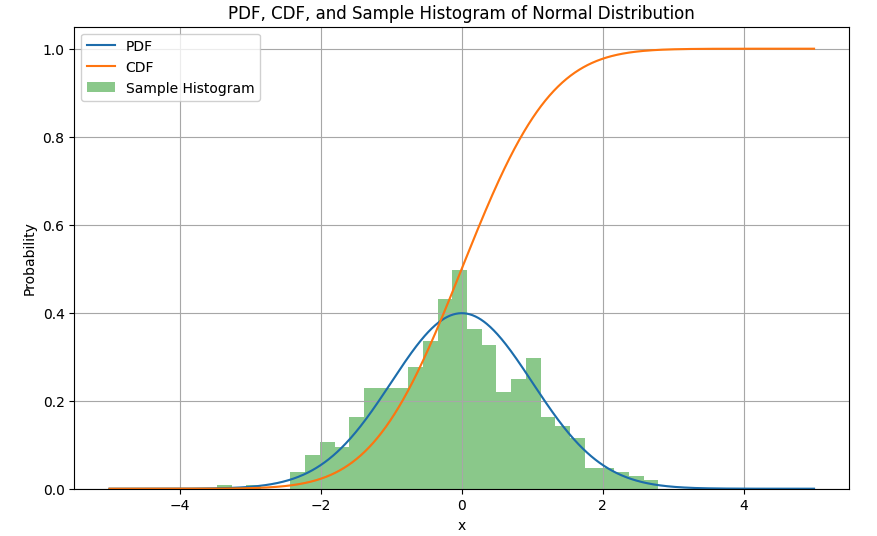

在這個例子中，pdf 和 cdf 是根據模型預測的值，而 sample 是隨機模擬出的值，用於檢驗模型與實際數據的符合程度。

PDF 與 sample的分佈是一致。CDF（累積分佈函數）代表的是在某個數值之前的累積概率。對於正態分佈來說，當 x 值由-5往0時越接近平均值，累積概率越接近 0.5，這是因為正態分佈是對稱的, CDF在 x > 0 的區間，CDF 的值持續上升，而是趨於 1。這種情況下，如果模型的預測與實際數據相符，並且實際數據的分佈也表現出在這個區間的數值較大的趨勢，那麼可以認為模型是比較正確的